Teorema Di Pitagora Scuola Primaria cardays


Il caso del teorema di pitagora

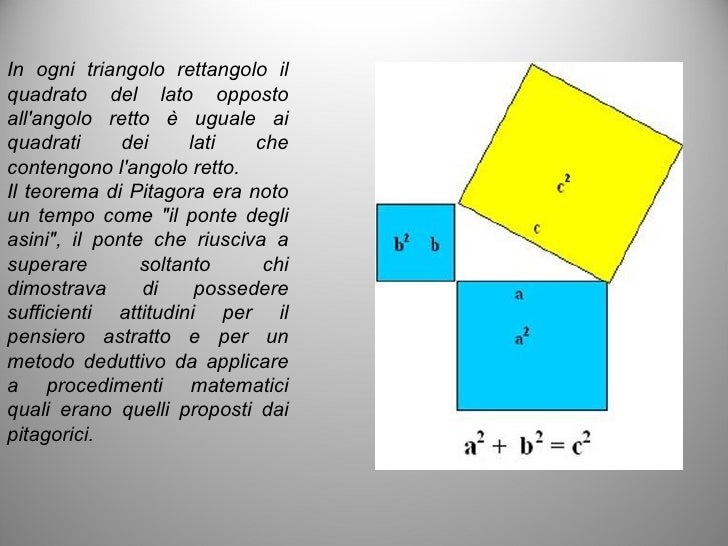
Il teorema di Pitagora si applica ai triangoli rettangoli, cioè ai triangoli che hanno un angolo di 90 gradi. L'enunciato del teorema è il seguente: In un triangolo rettangolo, l'area del quadrato costruito sull'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma delle aree dei quadrati costruiti sugli altri due lati. a2 + b2.


Teorema di Pitagora Esempio 2 YouTube

Teorema di Pitagora: le formule. Quali sono le formule del teorema di Pitagora? Dati gli enunciati che abbiamo precedentemente esposto, è possibile ricavare le formule direttamente da lì. i2 = c12 +c22 i 2 = c 1 2 + c 2 2. Una volta compresa questa relazione tra i dati è possibile ricavare velocemente anche le formule inverse del teorema di.


Teorema di Pitagora Lettera43

e l'enunciato del teorema di Pitagora si può esprimere come: \[ \boxed{a^2 = b^2 + c^2} \] Si hanno anche le seguenti formule inverse:. Per chi ancora non ha visto il calcolo letterale, la spiegazione sotto spoiler disponibile a seguire dovrebbe essere di aiuto. Precisiamo per questi lettori che l'operazione di moltiplicazione si può.


2.1 Il teorema di Pitagora YouTube

Video sulla spiegazione con dimostrazione del Teorema di Pitagora per ragazzi di seconda media00:00:00 | Introduzione00:00:51 | Enunciato00:01:16 | Dimost.


Problemi con il teorema di Pitagora parte 1 YouTube

Una spiegazione semplice ed esauriente di una delle "leggi" matematiche più importanti. Pronti a usare carta, matita e forbici? Prima di parlare del celebre Teorema di Pitagora, occorre ricordare un paio di cose riguardanti i triangoli. PREMESSA. Tra tutti i triangoli infatti, uno ha molte proprietà utili e interessanti: il triangolo.


17. Trapezio isoscele 1 Teorema di pitagora, Matematica scuola media, Scuola media

Teorema di Pitagora: dall'enunciato alla dimostrazione facile In questo articolo troverai l'enunciato e le formule del famoso Teorema di Pitagora. E' importante che tu conosca e sappia usare bene il Teorema di Pitagora in quanto è fondamentale per lo studio della geometria, della geometria sul piano cartesiano e della trigonometria.Nonostante sia un argomento molto studiato a scuola, è.


Semplice spiegazione del teorema di Pitagora

TEOREMA (di Pitagora): Dato un triangolo rettangolo ABC AB C come in figura, allora vale la relazione a^2 + b^2 = c^2 a2 + b2 = c2 dove c c è l'ipotenusa del triangolo e b, a b,a sono i cateti. Da questo teorema si possono ricavare le seguenti formule, che permettono di ricavare la misura di un lato a partire dagli altri due:


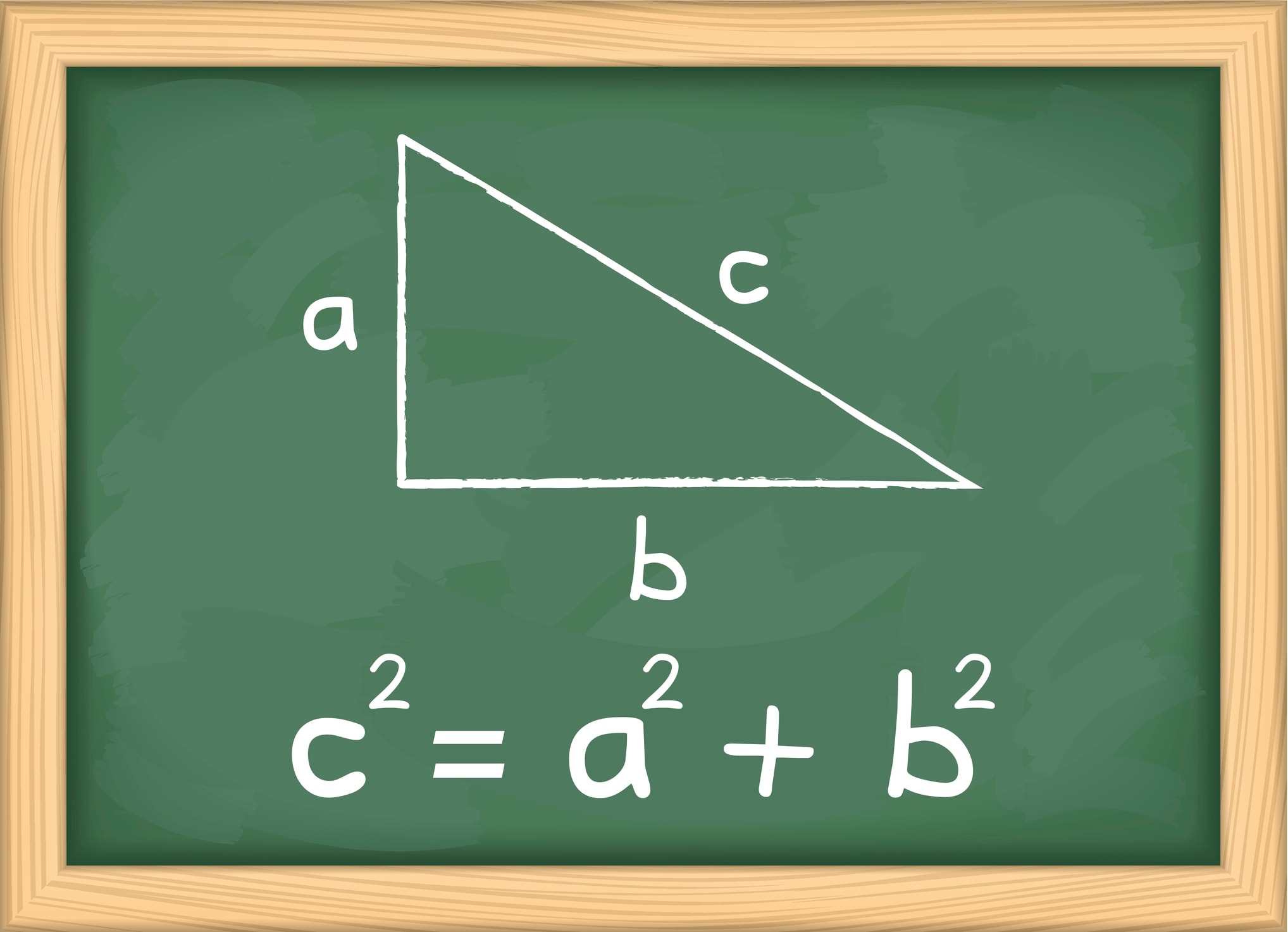
Teorema di Pitagora spiegazione ed esercizi Studenti.it

Introduzione al Teorema di Pitagora, formule e spiegazione. Per alunni di scuola secondaria di primo grado. Comprendere l'utilizzo del Teorema di Pitagora co.


Teorema di pitagora formule

La formula del Teorema di Pitagora. Il Teorema di Pitagora dice, in formula, che. AB² = AC² + BC². In numeri, riprendendo l'esercizio di prima, abbiamo dunque che 25 = 9 + 16, ossia 25 = 25. Quindi il matematico greco aveva proprio ragione! Ponendo AB = c, AC = a e BC = b,


14. Applicazioni del teorema di Pitagora sul quadrato Teorema di pitagora, Matematica scuola

Supponiamo di avere a (cateto minore) e c (ipotenusa). Per ricavare b (cateto maggiore): a2 + b2 = c2. a2 + b2 - c2 = 0. c2 - a2 - b2=0. c2 - a2 = b2. √c2 - a2 = b2. Per semplificare vedremo ora un esempio più concreto per l'applicazione del teorema di Pitagora. Immaginiamo un triangolo rettangolo di cui siano note la misura dell.


Teorema di Pitagora in 5 minuti (con dimostrazione) YouTube

Una generalizzazione del teorema di Pitagora è il teorema del coseno, che si applica ad un triangolo qualsiasi (non necessariamente retto).In un triangolo con vertici e angoli indicati come in figura, vale l'uguaglianza: ¯ = ¯ + ¯ ¯ ¯ ⁡. Nel caso in cui sia retto, vale ⁡ = e quindi l'enunciato è equivalente al teorema di Pitagora. Il termine aggiuntivo può essere interpretato come.


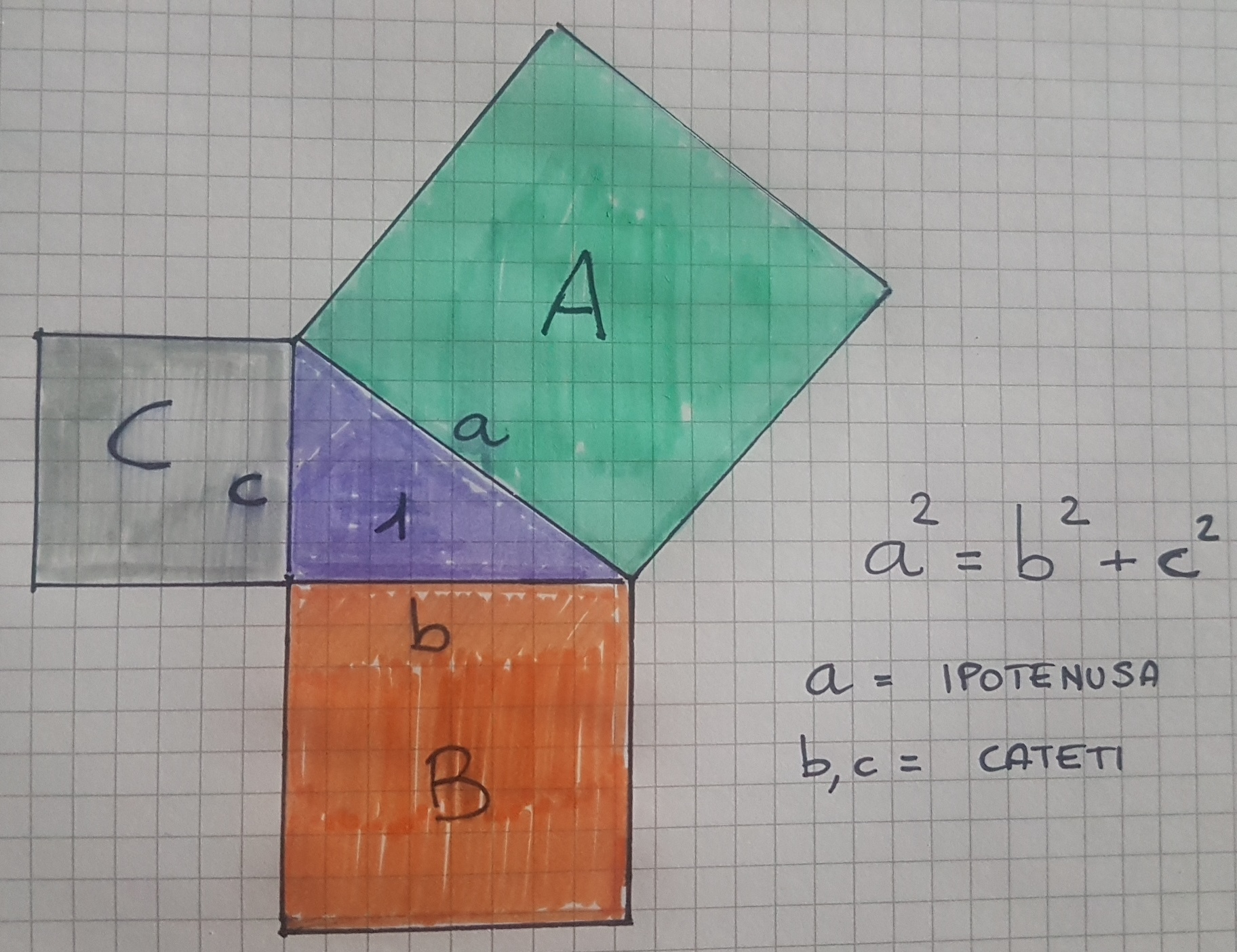
TEOREMA DI PITAGORA lezioniignoranti

In questo video scopriremo insieme il teorema di Pitagora, che troverai in tutta la tua carriera scolastica.Tutti i miei contenuti sono gratuiti: se volessi.


Il teorema di Pitagora un'applicazione pratica! YouTube

Adesso ci rimane da calcolare l'Area del quadrato Q_2 Q2 che ha come lato il cateto maggiore C del triangolo. Q_2= C \cdotp C = C^2 Q2 = C ⋅C = C 2. Abbiamo calcolato l'Area di tutti e 3 i quadrati. Adesso ritorniamo alla formula che Pitagora trovò, ossia: Q=Q_1 + Q_2 Q = Q1 +Q2.


Il Teorema Di Pitagora 2ª Media Primaria school, italiano, english, greek

Teorema di Pitagora - Formule e spiegazione. Appunto di geometria che spiega in modo semplice la definizione del Teorema di Pitagora con disegni, esempi e formule. Intorno al 2900 a.C gli antichi Egizi scoprirono che per alcune terne di numeri, a, b, c, corrispondenti alle misure dei lati di un triangolo rettangolo si verifica che: A² + B² = C².


Teorema di Pitagora YouTube

Con questa lezione il corso di Geometria Piana arriva a un risultato fondamentale: il teorema di Pitagora.La spiegazione si rivolge agli studenti delle Scuole Medie e delle Scuole Superiori ma è utile a tutti, perché in Geometria le applicazioni del teorema che stiamo per presentarvi sono numerosissime.


Formule Teorema di Pitagora per Medie Redooc

Visite: 24421. Uno dei teoremi più famosi di tutta la Geometria Euclidea è il Teorema di Pitagora. Esso afferma che il quadrato costruito sull'ipotenusa di un triangolo rettangolo è equivalente alla somma dei quadrati costruiti sui cateti del triangolo considerato. La sua dimostrazione viene attribuita, come dice il nome, al matematico.